arduino-tutorial-es
23 - Módulo sensor digital de temperatura
En este tutorial aprenderemos a utilizar el módulo de temperatura digital KY-028, un sensor que nos permite medir la temperatura ambiente de forma precisa y económica. Este módulo utiliza un termistor NTC (Negative Temperature Coefficient) que cambia su resistencia según la temperatura, permitiéndonos obtener lecturas tanto digitales como analógicas.
Material
| Imagen | Descripción |
|---|---|
 |
Arduino Uno o equivalente. |
 |
Protoboard |
 |
Cables de conexión |
 |
Módulo sensor temperatura KY028 |
Finalidad
En este experimento, aprenderemos a usar el módulo de temperatura digital y el módulo de temperatura analógico.
Módulo de temperatura digital
Módulo de detección de temperatura usando un termistor NTC. La señal de salida en ‘DO’ cambia a nivel alto cuando se alcanza la temperatura preestablecida (ajustable). Una señal de salida analógica del sensor está disponible en el pin ‘AO’.

Especificaciones
Este módulo consta de un termistor NTC, un comparador diferencial dual LM393, un potenciómetro de ajuste, 6 resistencias, 2 LED y 4 pines de cabecera macho. El módulo cuenta con salidas analógicas y digitales.
- Voltaje de funcionamiento: 3,3 V ~ 5,5 V
- Rango de medición de temperatura: -55 °C a 125 °C
- Precisión de medición: ±0,5 °C
- Dimensiones de la placa: 15 mm x 36 mm
Configuración de pines
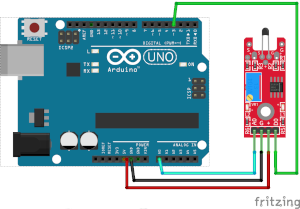
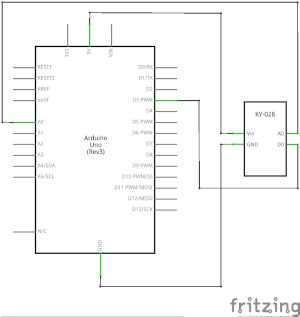
Conecte la salida analógica (A0) de la placa al pin A0 del Arduino y la salida digital (D0) al pin 3. Conecte la línea de alimentación (+) y tierra (G) a 5V y GND respectivamente.
| Módulo | Arduino |
|---|---|
| A0 | Pin A0 |
| G | GND |
| + | +5V |
| D0 | Pin 2 |
¿Qué es un termistor NTC?

Los termistores son elementos sensores de temperatura hechos de material semiconductor que ha sido sinterizado para mostrar grandes cambios de resistencia en proporción a pequeños cambios de temperatura.
Esta resistencia se puede medir utilizando una corriente continua pequeña y medir, o cc, que pasa a través del termistor para medir la caída de voltaje producida.
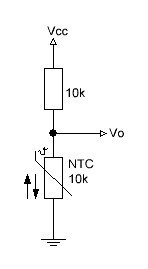
Los termistores NTC son resistencias no lineales que alteran sus características de resistencia con la temperatura.
La resistencia de NTC disminuirá a medida que aumente la temperatura. La forma en que la resistencia disminuye está relacionada con una constante conocida en la industria electrónica como beta o ß. Beta se mide en °K.
El Arduino tiene varios puertos ADC que podemos usar para leer un voltaje, o más bien un ‘valor ADC’. Si el puerto analógico está conectado a Vcc, el valor máximo que se lee es 1023 y, por supuesto, cuando está conectado a tierra es 0.
Ahora, si hacemos un divisor de voltaje que típicamente son dos resistencias en serie entre Vcc y tierra y el puerto analógico en el medio, la lectura dependerá de la relación de las dos resistencias, si son iguales, la lectura será 512, a la mitad de 1023. Si una de las resistencias, digamos que la inferior es un NTC, las lecturas en el puerto analógico variarán con la temperatura. Si la temperatura baja, el valor de la resistencia aumenta y también lo hará la lectura en el puerto analógico.
Supongamos que tenemos una resistencia Serie 10k y un NTC que por ahora decimos ‘R’.
Entonces el voltaje que se puede medir en el medio es
\[V_{o}=\frac{R}{R + 10K} \cdot V_{cc}\]Sin embargo, las lecturas del puerto analógico no dan un voltaje sino un valor ADC que se puede calcular fácilmente.
\[Valor ADC = 1023 \cdot \frac{V_{o}}{V_{cc}}\]si, por ejemplo, Vo = 4 voltios, el ADC = 818 o el valor ADC = 1023 *(Vo/VCC)
Si ahora combinamos las dos fórmulas o, como se dice, ‘sustituimos’ Vo en la fórmula para ADC, obtenemos lo siguiente:
\[Valor ADC= \frac{R}{R + 10K} \cdot V_{cc} \cdot \frac{1023}{Vcc}\]A medida que multiplicamos por Vcc pero también dividimos por Vcc, podemos sacar esto de la ecuación y terminar con
\[Valor ADC= \frac{R}{R + 10K} \cdot 1023\]si queremos sacar el valor de R de esta ecuación, esto se convierte en
\[R = \frac{10K}{(\frac{1023}{ADC}-1)}\]Entonces, siempre que sepamos el valor de la resistencia en serie, podemos calcular el valor del NTC a partir del valor ADC medido. Ahora recuerde, esto es válido para una configuración pull-up. Si se trata de una configuración pull-down, el cálculo del valor del ADC a la resistencia es el inverso.
$R_{ntc} = 10K \cdot (\frac{1023}{ADC}-1)$; para la configuración pull-down
$R_{ntc} = 10K / (\frac{1023}{ADC}-1)$; para la configuración pull-up
Entonces, ¿cómo se vería esto en un programa?
//Midiendo el valor de resistencia de NTC
byte NTCPin = A0;
const int SERIESRESISTOR = 10000;
void setup()
{
Serial.begin(9600);
}
void loop()
{
float ADCvalue;
float Resistance;
ADCvalue = analogRead(NTCPin);
Serial.print("Analógico ");
Serial.print(ADCvalue);
Serial.print(" = ");
//convertir el valor en resistencia
Resistance = (1023 / ADCvalue) - 1;
Resistance = SERIESRESISTOR / Resistance;
Serial.print(Resistance);
Serial.println(" Ohm");
delay(1000);
}
Conocer la resistencia del NTC es bueno pero no nos dice mucho sobre la temperatura… ¿o sí?
Bueno, muchos NTC tienen un valor nominal que se mide a 25 ºC, por lo que si tiene un NTC de 10k y mide 10k, esto significa que hay 25ºC en este momento. Esto no te ayuda mucho cuando la medida es diferente.
Podría mantener una tabla en la que cada valor de resistencia represente una temperatura. Estas tablas son muy precisas pero requieren mucho trabajo y espacio de memoria.
Sin embargo, hay una fórmula, la ecuación de Steinhart-Hart, que hace una buena aproximación para convertir los valores de resistencia de un NTC en temperatura. No es tan exacta como la tabla de termistores (después de todo, es una aproximación), pero es bastante precisa.
La ecuación de Steinhart-Hart se ve así:
\[{\frac{1}{T} = {A + {B \cdot \ln}}{(R)} + {C \cdot {({\ln{(R)}})}^{3}}}\]Esta es una ecuación bastante compleja que requiere varios parámetros (A, B, C) que normalmente no tenemos para el funcionamiento del NTC. Hay dos cosas que podemos hacer. Podemos tomar 3 lecturas con una temperatura calibrada y luego calcular los parámetros A, B y C.
\[{\begin{bmatrix} 1 & {\ln{({R1})}} & {({\ln{({R1})}})}^{3} \\ 1 & {\ln{({R2})}} & {({\ln{({R2})}})}^{3} \\ 1 & {\ln{({R3})}} & {({\ln{({R3})}})}^{3} \\ \end{bmatrix} \cdot \begin{bmatrix} A \\ B \\ C \\ \end{bmatrix}} = \begin{bmatrix} \frac{1}{T_{1}} \\ \frac{1}{T_{2}} \\ \frac{1}{T_{3}} \\ \end{bmatrix}\]pero afortunadamente hay una simplificación de esta fórmula, llamada Ecuación del parámetro B. Esta se ve de la siguiente manera:
\[{\frac{1}{T} = {\frac{1}{T_{0}} + {\frac{1}{B} \cdot \ln}}}{(\frac{R}{R_{0}})}\]T~0~ es la temperatura nominal, 25 °C en Kelvin (= 298,15 K). B es el coeficiente del termistor (3950 es un valor común). R~o~ es la resistencia nominal del NTC (por lo tanto, a 25ºC). Digamos que tenemos un NTC de 10Kohm. Solo necesitamos sustituir R (la resistencia medida) para obtener T (temperatura en Kelvin) que luego convertimos a °C.
Código
Código ARD023
byte NTCPin = A0;
#define SERIESRESISTOR 10000
#define NOMINAL_RESISTANCE 10000
#define NOMINAL_TEMPERATURE 25
#define BCOEFFICIENT 3950
void setup()
{
Serial.begin(9600);
}
void loop()
{
float ADCvalue;
float Resistance;
ADCvalue = analogRead(NTCPin);
Serial.print("Analógico ");
Serial.print(ADCvalue);
Serial.print(" = ");
//convertir valor a resistencia
Resistance = (1023 / ADCvalue) - 1;
Resistance = SERIESRESISTOR / Resistance;
Serial.print(Resistance);
Serial.println(" Ohm");
float steinhart;
steinhart = Resistance / NOMINAL_RESISTANCE; // (R/Ro)
steinhart = log(steinhart); // ln(R/Ro)
steinhart /= BCOEFFICIENT; // 1/B \* ln(R/Ro)
steinhart += 1.0 / (NOMINAL_TEMPERATURE + 273.15); // + (1/To)
steinhart = 1.0 / steinhart; // Invertir
steinhart -= 273.15; // convertir a C
Serial.print(steinhart);
Serial.println(" oC");
delay(1000);
}
Montaje